Why ReLU Activation?
Problems with the linear, sigmoid and tanh activation

Following questions will be covered in this blog
- What is ReLU function
- Why not linear activation
- How ReLU activation generates non-linear hyperplane
- Why not sigmoid / tanh activation
We all have used ReLU activation while training a Neural network and have experienced that the trained model performs very well on test data but have you ever imagined how this model predicts the label and how the model decides hyperplane.
Well later in this blog we will visualize the hyperplane for a simple 2D example. Let’s first understand what ReLU activation is.
What is ReLU function
ReLU stands for Rectified Linear Unit.


That’s it.
Why not linear activation
When I started learning about neural networks I often wondered, if we already have linear function then why we needed a new function like ReLU in the first place. Let’s understand why linear activation will not work.
For simplicity we will consider a very simple 2D data set which looks like this

here cross represents class 1 data and circle represents class 0 data. Let’s consider a very simple neural network with only one hidden layer and with 2 units.

Now we will train this neural network with the above dataset. I am assuming that you already know how the weights update in the training phase and how backpropagation works. Note that f_1 and f_2 can be any activation which is linear activation in this example but f_3 must be sigmoid activation because we are building a binary class classifier. Since we are using linear activation, output of linear activation will look like this

Bias term will be there as well but let’s ignore it for now. Before going further I want to explain one more important concept related to linear algebra.
Let’s try to plot a line with slope = -1 and y_intercept = 1. It will look like this

w is a weight vector which is [1,1] in this case. Any data point above the hyperplane will generate positive value for y and data points below the hyperplane will generate negative value. In other words points which are in the direction of w will generate positive value and points which are in the opposite direction of w will generate negative value.
Final output will be given by
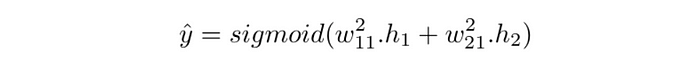
again, bias term will be there as well but we will ignore it just to make math simpler.

We want final output to be greater than 0.5 for all the data points belonging to class 1 and final output to be less than 0.5 for all the data points belonging to class 0. In other words input to the sigmoid should be large positive for class 1 data and large negative for class 0 data.
Now let’s visualize two hyperplanes corresponding to two hidden units.

h1 and h2 are two hyperplanes that represent f1 and f2 from the hidden units (h1 and h2 are not the exact hyperplane that you get after training. I am choosing this to make explanation easy ). I have also added three new test data points. One from class 1 and two from class 0.
Case 1:
Let’s calculate the predicted class for p1. Since p1 is in the direction of w1 and w2, both h1 and h2 will generate positive value for p1 and to make the final prediction greater than 0.5 we have to assign both w²_11 and w²_21 with positive value. By assigning both w²_11 and w²_21 with positive value all the data points that is in the direction of w1 and w2 will be correctly classified.
hurre…:)
We are not yet done.
Now calculate the predicted class for p2 with the same weights assigned for p1. hyperplane h1 will generate a small negative value as p2 is in the opposite direction of w1 and close to h1 and h2 will generate a large positive value as p2 is in the direction of w2 and far from h2.
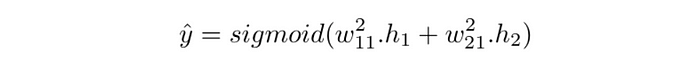
As far as p2 is concerned one can calculate that overall input to the sigmoid will be positive and final output will be greater than 0.5. Here p2 will be misclassified as predicted class is 1.
Now you can try with different combinations of w²_11and w²_21. No matter what the values are for those weights, you will end up with at least one misclassification. Here is the reason why.
If you look carefully, the input to the sigmoid is the linear combination of two hyperplanes. Think of it as the addition of two lines and the addition of two lines can never be a nonlinear function.
The main idea behind using a neural network is to learn the complex pattern from training data and to capture those information the model must produce nonlinearity. No matter what the size of the hidden layer and hidden units, if you use linear activation then you will end-up with only one linear function.
How ReLU activation generates non-linear hyperplane
To understand this we will use the same data set and same neural network architecture but now the activation function will be ReLU. Now suppose that we have trained the model and end-up with the same hyperplanes that we got for linear activation.

I have divided the entire space into four regions and placed one test point in each region. One more thing to notice that I have changed the direction of w1 and w2, we will see why.
Now output of ReLU activation is straight forward, it generates positive value for the points which are in direction of weight vector w.
Case 1 : Region 1
We want final output to be greater than 0.5 for all the data points from region1. Since p1 is in the opposite direction of w1 and w2 so both the hidden units will generate zero.
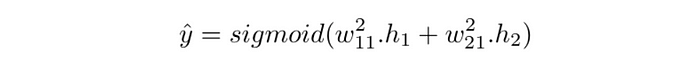
Input to the sigmoid function is zero so the final output will be 0.5. If we consider all the data points for which final output greater than 0.5 including 0.5 then region1 data will be correctly classified as class 1.
hurre….:)
Case 2 : Region 3
Till now we correctly classified region1 data points without making any constraints on w²_11and w²_21. We want final output to be less than 0.5 for all the data points from region3 . Test data p3 is in region3 and it is in the direction of both the weight vector w1 and w2 so output will be positive for both the hidden units. Now if we assign both w²_11and w²_21 with negative values then input to sigmoid function will become negative and final output will be less than 0.5. In this way region3 data points will be correctly classified as class 0.
Case 3 : Region 2 and Region 4
Data points belonging to region2 and region4 will be in the direction of one of the weight vector and in the opposite direction to the other weight vector. For data point p2, h1 will generate positive value but h2 will generate zero. Similarly for data point p4 , h2 will generate positive value and h1 will generate zero. Since we assigned both w²_11and w²_21 with negative values, input to sigmoid will become negative hence the final output will be less than 0.5 and correctly classified as class 0.
Finally the simple neural network having one hidden layer with two units and with ReLU activation will generate a nonlinear hyperplane which will look like this.

Why not sigmoid or tanh activation
In this section we will understand what are the consequences we might face if we use sigmoid / tanh activation and solution for that.
Consider a deep neural network with lots of hidden layers.

Above neural network is not that deep but good enough to explain. We updates the weights of neural network using this equation

where n is learning rate which decides what fraction of gradient term should be used for updation.
Now let’s expand the gradient term considering above neural network

If we will use sigmoid activation

The maximum value of the derivative of sigmoid is around 0.25 that means each derivative term will lie between 0 and 1 and we are taking product of these terms. As the number of hidden layers increases, the number of derivative terms will also increase. Finally the amount of update (second term in update equation) will become negligible and no matter what the loss is, those weight stops updating. This phenomenon is called the vanishing gradient problem.
The same problem will occur if we use tanh activation

Solution for the vanishing gradient problem is to use ReLU activation. Sigmoid and tanh activation captures nonlinear patterns of data and can be used for shallow neural networks but as long as deep neural networks are concerned , ReLU activation is preferred.

Derivative of the ReLU function will be either 0 or 1. No matter how deep the neural network are, ReLU activation converges the weights much faster than sigmoid or tanh function.
I hope all the four questions that I stated at the top of this blog is answered by now.
